Boolean Logic Explained: AND, OR, NOT for Beginners

Whether you realize it or not, you use Boolean logic daily. By saying “I do NOT want that” or “I like this AND that,” you use Boolean expressions. Assuming you accessed this article through a digital device, you have caused your device to use Boolean logical operators in processing information to get you to where you are. Boolean logic consists of two possible values: true and false. This is why Boolean logic (and binary logic) is considered true/false logic. For example, if someone asked you if you like ice cream, if you were using Boolean logic, you could say “yes” or “no” (yes being true and no being false). A few operators commonly used for boolean operations are NOT, AND, and OR. Let's dive into the basics of Boolean logic for beginners.

The Three Most Important Boolean Operators

Boolean operations are the foundation of logic in digital computers and everyday decisions. Explain simply, Boolean operations work with values that can be either true or false, also commonly represented as 1 (true) and 0 (false). The three most basic and important Boolean operations are AND, OR, and NOT.

AND Operator

The AND operation checks if two or more conditions are true. If every input is true, the output will also be true. If even one of the inputs is false, the entire statement becomes false. Consider this statement:

If I like ice cream AND cake, then I like ice cream cake.

Both conditions, liking ice cream and liking cake, must be true for the conclusion to be true. If you like only one of the two, the statement becomes false. In Boolean logic, this would look like:

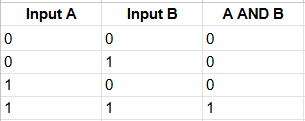
This table is called a truth table. The truth table for the AND operator shows that only when both A and B are 1 (true) does the output become 1.

OR Operator

The OR operation checks if at least one of the conditions is true. If either one (or both) inputs are true, the output will also be true. It only becomes false when both inputs are false. As an example:

If I like cookies OR brownies, then I'll be happy.

Even if you like just one of them, you'll still be happy. The only way you wouldn't be happy is if you didn't like either. Truth table for OR:

NOT Operator

The NOT operation is a bit different—it's a unary operator, meaning it works with only one input. NOT is the smallest of the Boolean logic operators. The NOT operation simply inverts the value it receives as input. If the input is true, it outputs false. If the input is false, it outputs true.

If I do not like broccoli, then I won't eat it.

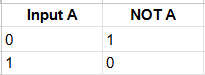
Here, liking broccoli is the input. The NOT operator flips that value. If you do like it (true), the NOT turns it into false (you won't avoid it). If you don't like it (false), the NOT turns it into true (you'll avoid it). The truth table for NOT is much simpler compared to AND and OR, because it has only one input:

If-Then Logic Format

Most Boolean operations can be described using an "if-then" format. These statements form the basic logic we use in everyday decisions and programming. For example:

If it's raining AND I forgot my umbrella, then I'll get wet.

This is a Boolean condition: two truths lead to a logical consequence. In digital computers, computing with logic gates, millions of decisions are made every second, all using this Boolean format.

Boolean Logic for Programmers

Boolean logic for programmers is very similar to the Boolean logic we use in everyday life. Boolean logic can be used in if-then statements and operations on variables in programming. The following code snippet checks if cakeLiked && (&& means and) iceCreamLiked are both true. If they are, then make iceCreamCakeLiked true as well.

if (cakeLiked && iceCreamLiked) {
    iceCreamCakeLiked = true;
}

The "!" in front of a piece of code is the same as a NOT operator. If you wanted to change the value of a Boolean variable to its inverse, you could write

x = false
x = !x

Now, after this operation, "x" equals true.

This is not a very in-depth explanation of Boolean logic in code. Check out our article on learning more about Boolean logic in programming.

Common Extra Symbols

In Boolean logic, a common symbol is a line over an operator, which looks like this: W̅. This means to perform the "not" operation on the value W. So if W equals 1, W̅ equals 0. This is one of the most common Boolean logic symbols in many circuit applications. Additionally, you may see a truth table that looks like this:

All the "X" means is that when the first column is at a "0" state, then the other columns are disabled, or in the don't care state, and do not matter. An example would be that the first column is the power connecting to the circuit, and when the circuit is powered off, then the other outputs will not do anything. Thus, they are in the "don't care" state.

Conclusion

Boolean logic is widely used in many aspects of programming and basic-level computer design. A good next step would be to learn more about the more complex Boolean operators used in computers as logic gates. Boolean logic forms the backbone of programming, digital electronics, and computer science. By mastering the fundamental Boolean operators, you'll be ready to explore more advanced topics like logic gates and digital circuits.

People also ask