Binary and Hexadecimal Conversions, Examples, and Tips for Beginners
Binary numbers are commonly referenced in the digital age, but many still don’t understand how they work. But what exactly is it? The binary number system explained simply is a base-2 number system. Our number system (1, 2, 3, 4, 5, etc.) is a base-10 system. Base-2 means that it only has two possible digits: 1 or 0. This is called true/false logic. If we have a perfectly good number system already in place, then why do we need a binary system? The reason lies in understanding how computers use binary with digital logic.
Digital Electronics
When someone says their device is digital, that means their device runs on Boolean logic. In the simplest terms, Boolean logic is a light switch. It is either on or off. There's no in between. Logic gates operate using Boolean logic, where inputs and outputs are either true or false. Essentially, digital computation means Boolean logic. You may have seen a connection between what you know about the binary system so far and Boolean logic. Boolean logic can only have 2 different states (on, off, true, false), and binary can also only have two states. This is known as digital logic. When I say digital logic is processing ones or zeroes, they aren’t literally processing ones and zeroes. A 1 represents a voltage running through a wire that is higher than the threshold voltage in a circuit. The threshold voltage is the minimum voltage that can be considered a “1”. Anything below, and it's a 0.
This creates 2 states, and is also why we use a base-2 system and not the common base-10. In digital logic, we don’t differentiate between 4 and 5 volts. This is how transistors work. Let’s dive into how to convert binary to decimal.
How to Convert Binary to Decimal
To learn how to convert decimal numbers to binary, it would be useful to realize how to convert binary numbers to decimal first. Let's say we are dealing with the binary number 1101. First, we take into account the number of digits in this number, which is 4. Then, from right to left, we add up the values according to their place in the number. The formula is:
Bit value • 2position
Starting from the rightmost bit (position 0) and using the value from that bit. In our example number, this would look like
1 • 20
because the digit value is 1, and we are at the first digit spot, giving us 20. If you're confused about why it is 20, you can think about how we determine decimal numbers. For the one place, we would use a number times 100, which equals the number we started with (5 • 100 = 5). Continuing with our binary number, we get a full equation of
1101 = 1 • 2³ + 1 • 2² + 0 • 2¹ + 1 • 2⁰ = 8 + 4 + 0 + 1 = 13
This works with any binary number. This number has four digits, so it can have 24 different combinations. One of those combinations is 0, so a four-digit binary number can be any whole number from 0 - 15. Here's a quick chart to help visualize the binary conversion from decimal

How to Convert Decimal to Binary
To convert decimal numbers to binary, we will look at the number 53. The method for this is dividing this number by two, and keeping the remainder separate from the result. Then, by looking at the remainders, we get the binary number. This is how it would look to perform this operation on 53:
53 ÷ 2 = 26 remainder 1 26 ÷ 2 = 13 remainder 0 13 ÷ 2 = 6 remainder 1 6 ÷ 2 = 3 remainder 0 3 ÷ 2 = 1 remainder 1 1 ÷ 2 = 0 remainder 1
Then, by looking at the remainders, the first binary digit is the last remainder, which was 1. Then we take the remainders in reverse order to get the number of
110101
We can double-check this work by converting this number back into decimal with the previous equation:
1 • 25 + 1 • 24 + 0 • 23 + 1 • 22 + 0 • 21 + 1 • 20 = 32 + 16 + 0 + 4 + 0 + 1 = 53
As you work more with binary numbers, it gets easier to find patterns in your head, and you can do almost all problems quickly and efficiently. My Grandma used to work at IBM, and she was able to add and subtract binary (in her head) faster than decimal. Practice helps a lot in all areas of life, but especially in math and science.
Hexadecimal Explained Simply
Hexadecimal (also called hex) is a base-16 number system, and it is used for simplifying binary code to a more readable (but still very difficult for large programs) format for humans. The possible characters are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Because the A-F digits aren't traditionally numbers, understanding hexadecimal as a beginner can be tricky. Here's a conversion table for the hex value and the corresponding decimal value:
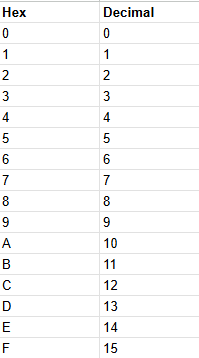
Choosing a base-16 system may seem odd, but think back to how many combinations 24 had. It had 16 total different combinations. Hexadecimal also has 16 total combinations. This makes it very easy to convert a binary number to hexadecimal. If you choose any 1 hexadecimal digit, let's say A, you can convert that directly into a 4-digit binary number. The value for the hex digit A in decimal is 10, and in binary, 10 is 1010. But let's say you were dealing with a byte of information, AA. Because we know an 'A' in hexadecimal is 1010, then this byte would equal 10101010 in binary. Knowing how to convert a hexadecimal number to binary is very important. This is because converting a hexadecimal number into decimal is a complicated process. We can still apply the same equation of binary to decimal, but we just change the base (2binary place) to 16.
How to Convert Hexadecimal to Decimal
To start, let's use AA. To convert AA to binary:
A (10) • 161 + A (10) • 160 = 160 + 10 = 170
This example was on the easier side for hexadecimal. With more digits, however, it gets more complex. For AAAA, you would have to do
10 • 163 + 10 • 162 + 10 • 161 + 10 • 160 = 40690 + 2560 + 160 + 10 = 43690
For this reason, hexadecimal is primarily used to shorten the length of binary numbers. When I am calculating a number in hexadecimal, I typically convert the number to binary first and then calculate the exact value.
How to Convert Decimal to Hexadecimal
As you probably could have guessed, to convert a decimal number to hexadecimal, you would divide the decimal number by 16 and separate the remainder until you get to 0. For a quick example, 53 would look like
53 ÷ 16 = 3 remainder 5 3 ÷ 16 = 0 remainder 3
And the result would be 05.
Conclusion
In conclusion, the binary number system and hexadecimal number system are both important to learn because of their prevalence in digital computations and data. In understanding how computers work, you would get lost without a basic understanding of binary numbers. Learning how to do basic arithmetic with binary and hexadecimal numbers is a fantastic way to get practice working with these systems. Computer architecture is a great next (but very big) step in applying the binary number system in real life. Binary and hexadecimal are essential number systems in computing. Binary represents the fundamental on/off nature of digital electronics, while hexadecimal offers a compact way to handle binary values. Mastering conversions between these systems helps in understanding data storage, computer architecture, and programming.